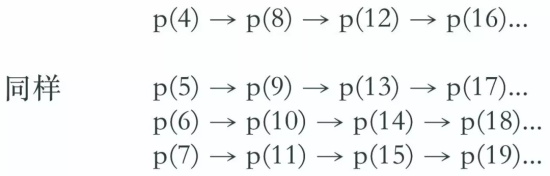久久99国产精品尤物-国产高清色播视频免费看-男生肌肌往女人桶爽视频-精品国产-91PORNY九色|www.jqdstudio.net

       編者按：移棋相間游戲最早被記載于我國清代康熙年間成書的筆記小說《堅瓠集》中，在日本和英國亦曾以“鴛鴦游戲”和“泰特問題”之名風行。它要求玩家將n個相鄰的白色棋子和n個相鄰的黑色棋子，通過移動相鄰兩子的方式得到“黑白相間”的結果。

《堅瓠集》中記錄，清代順治年間胡勵之曾發現當3≤n≤10時，經過n次移動均可得到“黑白相間”現象。數百年后的1920年代，是年尚在讀中學的數理統計學開創者之一、我國數學家許寶騄和他的好友、“新紅學”開拓者俞平伯在閱讀此書后，曾將上述規律推至二十棋子。許寶騄在一年后總結出“合四為一”的新規律，據稱一分鐘即可講完，使人豁然貫通。然而，由于后來科學研究任務繁重，許先生最終也未能如愿將這一公式整理出來。

而對這一游戲規律的探尋，也就一直傳承到了十余年后許寶騄任教的西南聯大學生身上。在本文中，世界著名物理學家、諾貝爾物理學家楊振寧先生完整記錄下了他對該問題“Modulo 4”解法的論證。

（圖源：pixabay.com）

撰文 | 楊振寧

1940年前后，在西南聯大物理系和數學系的師生們許多都喜歡玩一個移動2n個圍棋子的游戲。我也對它花過不少時間，始終未能完全解決。20多年后在美國我重新研究它，終于解決了所有n=3,4,5……的游戲，可是沒有把答案寫下來，只記得解決的一個關鍵方法是modulo 4。

最近看到一本關于許寶騄[1]的書，《道德文章垂范人間》，其中316頁上有一篇俞潤民的文章[2]，說許曾研究“移棋相間法”，曾發現“合四為一之新律”。我猜，此新律恐怕就是后來我發現的modulo 4方法。

這幾天重新研究此游戲，再度得到全解，在下面描述。

游戲初始：p(3)

六個棋子擺成一行，如 (1) ，黑子 (b) 在左，白子 (v) 在右。

然后移動最左二子至最右，成 (2) ，再移動二子成 (3) ，再移動二子成  (4)。

從 (1) 到 (4) ，三步移動，達到黑白相間是游戲 p(3) 的三步解。請注意，每次移動，必須是相鄰二子，平行移動。

p(4)

p(5)

p(6)

p(7)

p(8)

從 (31) 到 (39) 八步平行移動可以分成三段 ：

第一段  (31) 到 (33) 兩步。請注意中間八子 bbbbvvvv 完全不動。 

第二段  (33) 到 (37) 四步。請注意左右兩端的 bvvb 和 vvbb 八子完全不動。 

第三段  (37) 到 (39) 兩步。其中第一步先不動 (37) 的最左四子bvvb, 只把最右四子的中間二子 vb 移到左面，成 (38) 。第二步則把 (38)  中最左的 bv 二子移到右面成 (39) 。

極重要的比較 ：

比較第二段 (33) 到 (37) 這四步，與 p(4) 的 (5) 到 (9) 這四步，前者去掉最左四子與最右四子就與后者完全雷同！！！也是說 p(4) 是p(8) 的中心。p(8) 在中心以外還有第一段的兩步和第三段的兩步，以及左右八子，合起來形成一框，我們稱它為外框。

Modulo 4 p(8) 的中心是 p(4) 。四周是一個外框。我們把此關系寫為

p(4)  →  p(8)

這個關系顯然可以推廣 ：

至此我們已顯示所有 n>3 時 p(n) 的解法。

注解

[1] 數理統計學起源于二十世紀前半葉。創建此學科的五、六位學者中有許寶騄。

[2] 俞潤民是許寶騄的外甥，是俞平伯的兒子。俞文還說此游戲“始于清順治六七年”。

2019年11月完稿于清華園

來源于數學文化 ，作者楊振寧