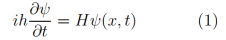久久99国产精品尤物-国产高清色播视频免费看-男生肌肌往女人桶爽视频-精品国产-91PORNY九色|www.jqdstudio.net

張奠宙：楊振寧講（經典）數學笑話兼論數學和物理的關系

點擊：  作者：張奠宙    來源：和樂數學微信號  發布時間:2024-02-16 11:39:04

 

 

楊振寧是當代的大物理學家, 又是現代數學發展的重要推動者, 他的兩項巨大成就: 楊–密爾斯規范場和楊–巴克斯特方程, 成為80年代以來一系列數學研究的出發點, 其影響遍及微分幾何、偏微分方程、低維拓撲、辮結理論、量子群等重大數學學科。筆者曾在「楊振寧與當代數學」的訪談錄中有過較為詳細的介紹(此文的中文版在臺灣「數學傳播」1992年4月發表, 內容不全相同的英文版刊于「Mathematical Intelligencer」Vol.15,NO。.4,1993。它的中譯文已被收入楊振寧的新著「讀書教學再十年」(臺灣時報出版公司,1995), 這里記錄的有關數學與物理學的關系, 來自筆者在1995年末在紐約州立大學(石溪) 訪問楊振寧先生時的一些談話材料, 因為不是系統的談話, 故稱「漫談」。

 

 

一.     有關數學的兩則「笑話」

 

1980年代初, 楊振寧曾在韓國漢城作物理學演講時說「有那么兩種數學書: 第一種你看了第一頁就不想看了, 第二種是你看了第一句話就不想看了」。當時引得物理學家們轟堂大笑。此話事出有因。1969年, 楊振寧察覺物理上的規范場理論和數學上的纖維叢理論可能有關系, 就把著名拓撲學家Steenrod著的「The Topology of Fibre Bundles纖維叢的拓撲)」[1]一書拿來讀, 結果是一無所獲。原因是該書從頭至尾都是定義、定理、推論式的純粹抽象演繹, 生動活潑的實際背景淹沒在形式邏輯的海洋之中, 使人摸不著頭腦。

 

上述漢城演講中那句話本來是即興所開的玩笑, 不能當真的。豈料不久之后被「Mathematical Intelligencer」捅了出來, 公之與眾。在數學界當然會有人表示反對, 認為數學書本來就應該是那樣的。不過, 楊振寧先生說「我相信會有許多數學家支持我, 因為數學畢竟要讓更多的人來欣賞, 才會產生更大的效果」。

 

我想, 楊振寧是當代物理學家中特別偏愛數學, 而且大量運用數學的少數物理學者之一。如果連他也對某些數學著作的表達方式嘖有煩言, 遑論其它的物理學家? 更不要說生物學家、經濟學家、一般的社會科學家和讀者了。

 

另一則笑話, 可在波蘭裔美國數學名家S.M.Ulam 的自傳「一個數學家的遭遇(Advantures of a mathematician) 」[2]中讀到。該書294頁上寫道: 「楊振寧, 諾貝爾物理學獎獲得者, 講了一個有關現時數學家和物理家間不同思考方式的故事: 一天晚上, 一幫人來到一個小鎮。他們有許多衣服要洗, 于是滿街找洗衣房。突然他們見到一扇窗戶上有標記:『這里是洗衣房』。一個人高聲問道: 『我們可以把衣服留在這兒讓你洗嗎?』窗內的老板回答說:『不, 我們不洗衣服。』來人又問道:『你們窗戶上不是寫著是洗衣房嗎』。老板又回答說: 『我們是做洗衣房標記的, 不洗衣服』。這很有點像數學家。數學家們只做普遍適合的標記, 而物理學家卻創造了大量的數學。」

 

楊振寧教授的故事是一則深刻的寓言。數學圈外的人們對數學家們「只做標記, 不洗衣服」的做法是不贊成的。數學家Ulam 在引了楊振寧的「笑話」之后, 問道, 信息論是工程師C. Shannon 創立的, 而純粹數學家為什么不早就建立起來? 他感嘆地說:「現今的數學和19世紀的數學完全不同, 甚至百分之九十九的數學家不懂物理。然而有許許多多的物理概念, 要求數學的靈感, 新的數學公式, 新的數學觀念。」

 

二.     理論物理的「猜」和數學的「證」

 

1995年12月, 楊振寧先生接到復旦大學校長楊福家的來信, 請楊振寧在1996年5月到復旦為「楊武之講座」做首次演講。楊武之教授是楊振寧的父親, 又是中國數學前輩,早年任清華大學數學系系主任多年, 五十年代后則在復旦大學任教授, 所以楊振寧很愉快地接受了邀請。但是他不能像楊福家校長要求的那樣做20次演講, 只準備講三次。順著這一話題, 楊振寧先生又談了理論物理和數學的一些關系。

 

楊先生說:「理論物理的工作是『猜』, 而數學講究的是『證』。理論物理的研究工作是提出『猜想』, 設想物質世界是怎樣的結構,只要言之成理, 不管是否符合現實, 都可以發表。一旦『猜想』被實驗證實, 這一猜想就變成真理。如果被實驗所否定, 發表的論文便一文不值(當然失敗是成功之母,那是另一層意思了)。數學就不同, 發表的數學論文只要沒有錯誤, 總是有價值的。因為那不是猜出來的, 而有邏輯的證明。邏輯證明了的結果, 總有一定的客觀真理性。」

 

「正因為如此, 數學的結果可以講很長的時間, 它的結果以及得出這些結果的過程都是很重要的。高斯給出代數學基本定理的五種證明, 每種證明都值得講。如果讓丘成桐從頭來講卡拉比(Calabi) 猜想的證明, 他一定會有20講。但是教我講『宇稱不守恒』是怎么想出來的, 我講不了多少話。因為當時我們的認識就是朝否定宇稱守恒的方向想,『猜測』不守恒是對的。根據有一些, 但不能肯定。究竟對不對, 要靠實驗。」

 

楊先生最后說:「理論物理的工作好多是做無用功, 在一個不正確的假定下猜來猜去,文章一大堆, 結果全是錯的。不像數學, 除了個別錯的以外, 大部分都是對的, 可以成立的」。

 

楊先生的這番話, 使我想起不久前Quine 和Jaffe 的一篇文章[4], 發表于Bulletin of AMS,1993年8月號, 曾引起相當的轟動。該文的主題是問「猜測數學是否允許存在? 」。其中提到, 物理學已經有了分工, 理論物理做「猜測」, 實驗物理做「證明」。但是數學沒有這種分工。一個數學家, 既要提出猜想, 又要同時完成證明。除了希爾伯特那樣的大人物可以提出23個問題, 其猜想可以成為一篇大文章之外, 一般數學家至多在文章末尾提點猜想以增加讀者的興趣, 而以純粹的數學猜想為主體的文章是無處發表的。因此, 兩位作者建議允許「理論數學」, 即「猜測數學」的存在。

 

這樣一來, 現在有兩種相互對立的看法。一方面, 物理學界中像楊振寧先生那樣, 覺得理論物理的研究太自由, 胡亂猜測皆成文章,認為數學還比較好的。另一方面, 數學界如Quine 和Jaffe 那樣, 覺得目前數學研究要求每個結論都必需證明的要求, 太束縛人的思想。應該允許人們大膽地猜測, 允許有根據而未經完全確認的數學結論發表出來。二者孰是孰非, 看來需要一個平衡。許多問題涉及哲學和社會學層面, 就不是三言兩語可以解決的了。

 

三.     復數、四元數的物理意義

 

 

虛數i=p

 

−1 的出現可溯源于15世紀時求解三次方程,但到18世紀的歐拉時代,仍稱之為「想象的數」(imaginary)。數學界正式接受它要到19世紀, 經Cauchy, Gauss, Riemann, Weierstrass 的努力, 以漂亮的復變量函數論贏得歷史地位。至于在物理學領域, 一直認為能夠測量的物理量只是實數,復數是沒有現實意義的。盡管在19世紀, 電工學中大量使用復數, 有復數的動勢, 復值的電流, 但那只是為了計算的方便。沒有復數,也能算出來, 只不過麻煩一些而已。計算的最

 

后結果也總是實數, 并沒有承認在現實中有真有「復數」形態的電流。鑒于此, 楊振寧先生說, 直到本世紀初,情況仍沒有多少改變。一個例證是創立量子電動力學的薛定諤(Schrodinger)[4]。1926年初, 據考證, 他似乎已經得到現在我們熟悉的方程

 

 

其中含有虛數單位i, ,  是復函數, 但最后總是取實部。薛定諤因其中含虛數而對(1) 不滿意, 力圖找出不含復數的基本方程。于是他將上式兩面求導后化簡, 得到了一個沒有虛數的復雜的高階微分方程

 

 

1926年的6月6日, 薛定諤在給洛蘭茲的一封長信中, 認為這一不含復數的方程(2) 「可能是一個普遍的波動方程。」這時, 薛定諤正在為消除復數而努力。但是, 到了同年的6月23日, 薛定諤領悟到這是不行的。在論文[5]中,他第一次提出: 「   是時空的復函數, 并滿足復時變方程(1)。」并把(1) 稱謂真正的波動方程。其內在原因是, 描寫量子行為的波函數, 不僅有振幅大小, 還有相位, 二者相互聯系構成整體, 所以量子力學方程非用復數不可。另一個例子是H.Weyl 在1918年發展的規范理論, 被拒絕接受, 也是因為沒有考慮相因子, 只在實數范圍內處理問題。后來由Fock 和London 用加入虛數i 的量子力學加以修改, Weyl 的理論才又重新復活。20 數學傳播21卷2期民86年6月牛頓力學中的量全都是實數量, 但到量子力學, 就必須使用復數量。楊振寧和米爾斯在1954年提出非交換規范場論, 正是注意到了這一點, 才會把Weyl 規范理論中的相因子推廣到李群中的元素, 完成了一項歷史性的變革[6]。1959年, Aharanov 和Bohm 設計一個實驗, 表明向量勢和數量勢一樣, 在量子力學中都是可以測量的,打破了「可測的物理量必須是實數」的框框[7]。這一實驗相當困難,最后由日本的Tanomura 及其同事于1982和1986先后完成[8]。這樣, 物理學中的可測量終于擴展到了復數。

 

令我驚異的是, 楊振寧教授預言, 下一個目標將是四元數進入物理學。自從1843年愛爾蘭物理學家和數學家Hamiton 發現四元數之后, 他本人曾花了后半輩子試圖把四元數系統, 像復數系統那樣地廣泛運用于數學和物理學, 開創四元數的世紀。但結果是令人失望的。人們曾評論這是「愛爾蘭的悲劇」[9]。時至今日, 一個大學數學系的畢業生可能根本不知道有四元數這回事, 最多也不過是非交換代數的一個例子而已。我還記起,1986年春, 錢學森在致中國數學會理事長王元的一封信中, 曾建議多學計算器知識, 而把研究「四元數解析」(復變函數論的推廣) 的工作貶為「像上一個世紀」東西。總之, 我和許多數學工作者一樣, 認為四元數發現, 只不過是「抽象的數學產物」, 不會有什么大用處的。

 

楊振寧向我解釋了他的想法: 物理學離不開對稱。除了幾何對稱之外, 還有代數對稱。試看四元數a+bi+cj+dk , 其基本單位滿足i^2 = j^2 = k^2 = −1 , 而ij = k, jk =i , ki = j ; ij = −ji , jk = −kj , ki =−ik 。像這種對稱的性質在物理學中經常可以碰到。問題是這種四元數的對稱還沒有真正用于物理現象, 而且物理現象中的一些對稱也還沒有找到基本的數學源由。最近, 丘成桐等人的文章[10]說:「我在1977年發表的一篇文章—Condition of Self-duality for SU(2) gauge fields on Euclidean fourdimensionalspace[11], 曾推動代數幾何中穩定叢的解析處理的理論。我還沒有問過數學家, 不知道這是怎么一回事。許多工作, 包括運用四元數表示的物理理論, 也許會在這種交流中逐步浮現的」。

 

楊振寧先生又說, 至于將復變函數論形式地推廣到四元數解析理論, 由于四元數乘積的非交換性, 導數無法唯一確定, 所以不會有什么好結果出來。現在也有物理學家寫成著作, 用四元數來描寫現有的物理定律, 就沒有引起什么注意。將來要用四元數表達的物理定律, 一定會是一組非線性微分方程組, 其解的對稱性必需用四元數來表示。所以, 楊先生相信:「愛爾蘭的悲劇是會變成喜劇的」。

 

四.     「雙葉」比喻

 

數學和物理學的關系, 應該是十分密切的。在數學系以外的課程中, 物理系開設的數學課最多最深。「物理學公理化, 數學化」, 曾是一個時期許多大學問家追逐的目標。不過, 擅長使用數學于物理的楊振寧教授卻認二者間的差別很大, 他有一個生動的「雙葉」比喻, 來說明數學和物理學之間的關系, 如下圖。他認為數學和物理學像一對「對生」的樹葉, 他們只在基部有很小的公共部分, 多數部分則是相互分離的。楊振寧先生解釋說: 「它們有各自不同的目標和價值判斷準則, 也有不同的傳統。在它們的基礎概念部分, 令人吃驚地分享著若干共同的概念, 即使如此, 每個學科仍舊按著自身的脈絡在發展。」[12]

 

 

參考數據

1. Steenrod, The Topology of Fibre Bun-dles, Princeton University Press, 1951

2. S.M. Ulam, Adventures of a Mathe-matician, Charles Scribner’s Sons, New York, 1976

3. Quine and Jaffe, Theoretical Mathe-matics: Toward a Cultural Synthsis of Mathematics and Theorectical Physics, Bulletin of Amer. Math. Soc., Vol. 29(1993),1-13.

4. 楊振寧: −1 的平方根, 復相位與薛定諤–在英國帝國大學記念薛定諤誕辰100周年大會上的演講, 1987, 收入「讀書教學又十年」,時報出版社, 1995, pp.41–56

5. Schrodinger, E Ann. D. Phys. 81 (109)(received June 23).

6. C. N. Yang and R. L. Mills, Con-versation of isotopic spin and iso-topic gauge invariance. Phys. REv. 96(1954), 191-195.

7. Y.Aharonov and D. Bohm, Phys. Rev. 115(1959),485.

8. A. Tonomura et al., Phys. Rev Lett. 48(1982),1443;56(1986),792.

9. E. T. Bell, Men of Mathematics, Dover Publications, New York, 1937.

10. J. A. Smoller, A. G. Wasserman, S.T. Yau:Einstein-Yang/Mills Black HoleSolutions. 「Chen Ning Yang–A Great Physicist of the Twentieth Century」.International Press, Hong Kong, 1995, pp. 209-221.

11. C. N. Yang, Condition of Self-duality for SU(2)gauge fields on Euclidian four-dimensional space, Phys. Rev. Lett.38, 1977, pp. 1377-1379.

12. C. N. Yang, Selected Papers, 1945-1980, with Commentary. W. H.Freedman and Company, San Fran-cisco, 1983.

 

原文標題：和楊振寧教授漫談: 數學和物理的關系，來自《數學傳播》。

 

作者：張奠宙 任教于中國上海華東師范大學；來源：和樂數學微信號