久久99国产精品尤物-国产高清色播视频免费看-男生肌肌往女人桶爽视频-精品国产-91PORNY九色|www.jqdstudio.net

陳省身演講：什么是幾何學？

點擊：  作者：陳省身    來源：賽先生 微信號  發布時間:2021-09-10 10:56:49

 

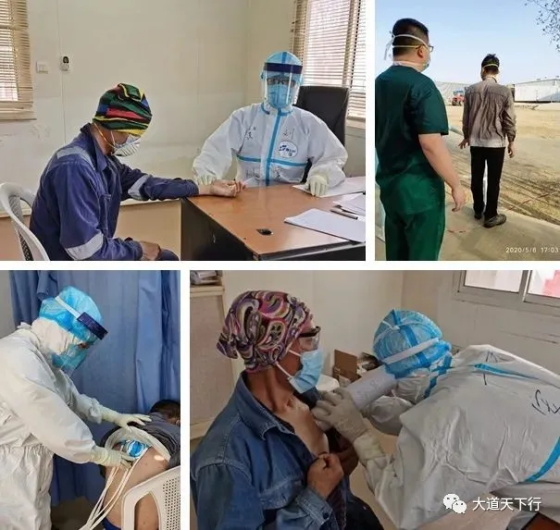
導讀：1999年求是獎頒獎會在復旦大學舉辦，求是科技基金會執委、顧問陳省身先生作了專題演講"什么是幾何學”。陳省身先生（1911年10月28日-2004年12月3日）是20世紀世界最重要的微分幾何學家之一、也是最有影響力的數學家之一，曾長期擔任加州大學伯克利分校、芝加哥大學數學教授。在即將迎來陳省身先生誕辰110周年紀念之際，《賽先生》今日分享這一高水平、有深度的演講，以饗讀者。本文源自求是科技基金會官網。

 

 

陳省身教授（左）與周光召教授（右）在介紹會中談笑甚歡，圖源：求是科技基金會官網。

演講 ｜ 陳省身

 

今天授獎的儀式很隆重，聽了許多人的演講，我非常感動。有機會在此演講，自己覺得非常之榮幸，也非常之高興。我想從現在起，我們就像平常上課一樣，不怎么嚴肅，隨便一點。我帶了一些材料，非常遺憾的是沒法投影。不投影也可以，我沒有什么準備。

 

大家希望我講一點幾何學，題目是《什么是幾何學》。我雖然搞了幾十年的幾何工作，但是很抱歉的一點是，當你們聽完演講后，不會得到很簡單的答案，因為這是一門廣泛而偉大的學問。在最近幾千年來，幾何學有非常重要的發展，跟許多其它的科學不但有關系、有作用，而且是基本的因素。

 

講到幾何學，我們第一個想到的是歐幾里德。除了基督教的《圣經》之外，歐幾里德的《幾何原本》在世界出版物中大概是銷售最多的一本書了。這本書在中國有翻譯，譯者是徐光啟與利瑪竇。徐光啟（1562~1633）是中國了不得的學問家，利瑪竇（M.Ricci）是到中國來的意大利傳教士。他們只翻譯了六章，中文本是在1607年出版的。

 

我們現在通用的許多名詞，例如并行線、三角形、圓周等這類名詞，我想都是徐光啟翻譯的。當時沒有把全書翻譯完，差不多只翻譯了半本，另外還有半本是李善蘭和偉烈亞力翻譯的。偉烈亞力（A.Wylie）是英國傳教士。很高興的是，李善蘭是浙江海寧人。海寧是嘉興府的一縣，我是嘉興人，所以我們是同鄉（掌聲）。對了，查濟民先生也是海寧人（掌聲）。

 

 

左起，查濟民董事長、周光召教授與楊振寧教授于介紹會中，圖源：求是科技基金會官網。

 

推動幾何學第二個重要的、歷史性發展的人是Descarte（1596~1650），中國人翻譯稱為笛卡兒。他是法國哲學家，不是專門研究數學的。他用坐標的方法，把幾何變成了代數。當時沒有分析或者無窮的觀念。所以他就變成代數。我想笛卡兒當時不見得覺得他這貢獻是很偉大的，所以他的幾何論文是他的哲學引里面最后的一個附錄，附屬于他的哲學的。

 

這個思想當然在幾何上是革命性的，因為當把幾何的現象用坐標表示出來時，就變成了代數現象。所以你要證明說一條直線是不是經過一個點，你只要證明某個數是不是等于零就行了。這樣就變成了一個簡單一點的代數問題。當然并不是任何的幾何問題都要變成代數問題，有時候變為代數問題后原來的問題更加復雜了。但這個關系是基本性的。

 

笛卡兒發現的坐標系，我們大概在中學念解析幾何都學到。有一點是這樣的（我的圖可惜現在沒法投影出來），給定一條直線，直線上有一個原點，其它的點由它的距離x來確定，然后經過x沿一定的方向畫一條直線，那么y坐標就是在那條線從x軸上這個點所經的距離，這就是笛卡兒的坐標，英文叫Cartesian，坐標。它的兩條線不一定垂直。不知道哪位先生寫教科書時把兩條線寫成垂直了，因此x坐標與y坐標對稱了。笛卡兒的兩個坐標不是對稱的，這是他非常重要的觀念，我們現在就叫纖維叢。

 

這些跟y坐標平行的直線都是纖維，是另外的一個空間。原因是這樣的：你把它這樣改了之后，那條直線就不一定要直線，可以是任何另外一個空間了。這樣可以確定空間里點用另外一組坐標來表示。所以有時候科學或數學不一定完全進步了，有時候反而退步了（笑聲）。笛卡兒用了這個坐標，就發現，我們不一定要用Cartesian坐標，可以用其它坐標，比如極坐標。

 

平面上確定一個點，稱為原點，過這點畫一條射線，稱為原軸。這樣平面上的點，一個坐標是這點與原點的距離，另外一個是角度，是這點與原點的連線與原軸的相交的角度，這就是極坐標。因此極坐標的兩個坐標，一個是正數或零，另外一個是從零到360度的角度。

 

當然我們都知道，還可以有許多其它的坐標，只要用數就可以確定坐標。因此，后來大家弄多了的話，就對幾何作出了另外一個革命性的貢獻，就是說，坐標不一定要有意義。只要每級數能定義一個點，我們就把它叫坐標。從而幾何性質就變成坐標的一個代數性質，或者說分析的性質。這樣就把幾何數量化了，幾何就變成形式化的東西了。

 

這個影響非常之大，當然這個影響也不大容易被接受，比如愛因斯坦。愛因斯坦發現他的相對論，特殊相對論是在1908年，而廣義相對論是在1915年，前后差了7年。愛因斯坦說，為什么需要7年我才能從特殊相對論過渡到廣義相對論呢？他說因為我覺得坐標都應該有幾何或物理意義。愛因斯坦是一個對學問非常嚴謹的人，他覺得沒有意義的坐標不大容易被接受，所以耽誤了他很多年，他才不能不接受，就是因為空間的概念被推廣了。

 

我忘掉了一段。我現在是講書，講書忘掉了補充一下是無所謂的，講錯了也不要緊（笑聲）。同樣我回頭再講一點歐幾里德。那時的歐幾里德的《幾何原本》并不僅僅是幾何，而是整個數學。因為那時候的數學還沒有發現微積分，無窮的觀念雖然已經有了，不過不怎么普遍。

 

我再說一點，就很可惜的是歐幾里德的身世我們知道得很少，只知道他大概生活在紀元前三百年左右。他是亞歷山大學校的幾何教授，他的《幾何原本》大概是當時的一個課本。亞歷山大大學是希臘文化最后集中的一個地方。因為亞歷山大自己到過亞歷山大，因此就建立了當時北非的大城，靠在地中海。但是他遠在到亞洲之后，我們知道他很快就死了。

 

之后，他的大將托勒密（PtolemySoter）管理當時的埃及區域。托勒密很重視學問，就成立了一個大學。這個大學就在他的王宮旁邊，是當時全世界偉大的大學，設備非常好，有許多書。很可惜由于宗教的原因，由于眾多的原因，現在這個學校被完全毀掉了。當時的基督教就不喜歡這個學校，已經開始被毀了，然后回教人占領了北非之后，就大規模地破壞，把圖書館的書都拿出來燒掉。所以現在這個學校完全不存在了。

 

幾何是很重要的，因為大家覺得幾何就是數學。比方說，現在還有這一印象，法國的科學院，它的數學組叫做幾何組。對于法國來講，搞數學的不稱數學家，而叫幾何學家，這都是受當時幾何的影響。當時的幾何比現在的幾何的范圍來得廣。不過從另一方面講現在的范圍更廣了，就是我剛才講到的坐標不一定有意義。一個空間可以有好幾種坐標，那么怎樣描述空間呢？這就顯得很困難啦，因為空間到底有什么樣的幾何性質，這也是一個大問題。

 

高斯與黎曼建立和發展了這方面的理論。高斯是德國人，我想他是近代數學最偉大的一個數學家。黎曼實際上是他的繼承人，也是德國教學家。他們都是哥廷根大學的教授。可惜的是黎曼活著時身體不好，有肺結核病，四十歲就死了。他們的發展有一個主要目的，就是要發展一個空間，它的坐標是局部的。空間里只有坐標，反正你不能講坐標是什么，只知道坐標代表一個點，所以只是一小塊里的點可以用坐標表示。因此雖然點的性質可以用解析關系來表示，但是如何研究空間這就成了大問題。

 

在這個之前，我剛才又忘了一個，就是基礎的數學是歐幾里德的書，但是歐幾里德的書出了一個毛病。因為歐幾里德用公理經過邏輯的手段得到結論。例如說，三角形三角之和一定等于180度，這是了不得的結果。歐幾里德可以用公理幾步就把它證明了，是一個結論。這個比現代的科學簡單得多了。

 

我們剛才聽了很多話，科學家做科學研究，第一樣就是跟政府要錢，跟社會要錢，說你給了我錢，我才能做實驗。當然實驗是科學的基礎。但是這樣一來就會有許多的社會問題和政治問題。

 

歐幾里德說，你給我一張紙，我只要寫幾下，就證明了這個結果。不但如此，我是搞數學的，我說數學理論還有優點，數學的理論可以預測實驗的結果。不用實驗，用數學可以得到結論，然后用實驗去證明。當然實驗有時的證明不對，也許你的理論就不對了，那當然也有這個毛病。

 

歐幾里德的公理是非常明顯的，但是他有一個有名的公理叫第五公設出了問題。這個第五公設講起來比較長，但是簡單地說，就是有一條直線與線外一點，經過這點只有一條直線與這條已給的直線平行。這個你要隨便畫圖的話，覺得相當可信。可是你要嚴格追問的話，這個公理不大明顯，至少不如其它公理這樣明顯。所以這個第五公設對當時數學界喜歡思想的人是個大問題。

 

當時最理想的情形是：第五公設可以用其它的公理推得，變成一個所謂的定理。那就簡單化了，并且可做這個實驗。我們搞數學的人有一個簡單的方法，就是我要證明這個公理，我先假定這個公理不對，看是不是可以得到矛盾。如果得到矛盾，就證明它是對的了。這就是所謂間接證明法。有人就想用這個方法證明第五公設，但是都失敗了。

 

我們現在知道這個第五公設并不一定對，經過一點的并行線可以有無數條，這就是非歐幾何的發現。非歐幾何的發現，它的社會意義很大，因為它表示空間不一定只有一個。西洋的社會相信上帝只有一個，怎么會有兩個空間，或者很多個空間呢？當時這是個很嚴重的社會問題。

 

不止是社會問題，同時也是哲學問題。像德國大哲學家康德，他就覺得只能有歐氏幾何，不能有非歐幾何。所以當時這是一個很大的爭論。非歐幾何的發現一個是J.Bolyai，匈牙利人，在1832年；一個是Lobachevski，俄國人，在1847年。

 

不過我剛才講到大數學家高斯，我們從他的種種著作中知道他完全清楚，但他沒有把它發表成一個結論，因為發表這樣一個結論，是可以遭到別人反對的。因此就有這么一個爭論。等到意大利的幾何學家Beltrami，他在歐幾里德的三維空間里造了一個曲面，曲面上的幾何就是非歐幾何，這對于消除大家的懷疑是很有利的工具。

 

因為上述結果是說，假定有一個三維的歐幾里德空間，就可以造出一個非歐幾何的空間來，所以在歐幾里德的幾何中亦有非歐幾何。你假定歐幾里德幾何，你就得接受非歐幾何，因此大家對非歐幾何的懷疑有種種的方法慢慢給予解除。

 

我剛才講到高斯與黎曼把坐標一般化，使坐標不一定有意義，這對幾何學產生的問題可大了。因為空間就變成一塊一塊拼起來的東西。那想怎么去研究它呢？怎么知道空間有不同的性質呢？甚至怎么區別不同的空間？

 

我這里有幾個圖，畫了幾個不同的空間，可惜我沒法把它投影出來。不過，總而言之空間的個數是無窮的，有很多很多不同的空間。現在對于研究幾何的人就產生一個基本問題，你怎樣去研究它。這樣一個基本的學問現在就叫Topology，拓樸學。

 

它是研究整個空間的性質，如什么叫空間的連續性，怎樣的兩個空間在某個意義上是相同的，等等。這樣就發展了許多許多的工具。這個問題也討論了。黎曼生活在1826~1866年。德國的教學制度在博士畢業之后，為了有資格在大學教書，一定要做一個公開演講，這個公開的演講就是所謂的Habilitationschrift。黎曼在1854年到哥廷根大學去做教授，做了一個演講，這個在幾何上是非常基本的文獻，就討論了這些問題。

 

如何研究這種空間呢？要研究這種空間，如果你只知道空間是隨便一塊塊拼起來的話，就沒有什么可以研究的了。于是你往往需要一個度量，至少你知道什么叫兩點之間的距離，你怎么去處理它呢？就需要解析的工具。往往你把距離表為一個積分，用積分代表距離。

 

黎曼的這篇1854年的論文，是非常重要的，也是幾何里的一個基本文獻，相當一個國家的憲法似的。愛因斯坦不知道這篇論文，花了七年的時間想方設法也要發展同樣的觀念，所以愛因斯坦浪費了許多時間。黎曼這篇論文引進的距離這個觀念，是一個積分，在數學界一百多年來有了很大的發展。

 

第一個重要的發展是黎曼幾何應用到廣義相對論，是相對論的一個基本的數學基礎。現在大家要念數學，尤其要念幾何學的話，黎曼幾何是一個最主要的部分，這個也是從黎曼的演講開始的。現在黎曼幾何的結果多得不得了，不但是幾何的基礎，可能也是整個數學發展的基礎。

 

 

1999年求是“杰出青年學者獎“得獎人于介紹會會場外合照，圖源：求是科技基金會官網。

 

我剛才提到一百多年來的發展。所謂的黎曼幾何實際上是黎曼的論文的一個簡單的情形，是某個情形。黎曼原來的意思，廣義下的意思，有個人做了重要的工作，是一個德國人Finsler。所以這部分的幾何就叫Finsler幾何。他在1918年在哥廷根大學寫了一篇博士論文，就講這個幾何。這個幾何后來發展不大多，因為大家不知道怎么辦。如果這個度量的積分廣了一點，對應的數學就變復雜了，不像黎曼的某個情形這樣簡單。

 

黎曼這情形也不簡單。黎曼普通地就寫了一個ds的平方等于一個兩次微分式，這個兩次微分式積分一下就代表弧的長度。怎樣研究這樣的幾何，這是需要一個像黎曼這種天才才有這個辦法。黎曼就發展了他所謂的Riemanncurvaturetensor，黎曼曲率張量。你若要搞這類幾何的話，就要有張量的觀念。而空間的彎曲性，這個彎曲性解析表示出來也比較復雜了，就是黎曼的曲率張量。

 

我們現在大家喜歡講得獎。我們今天發獎，有獎金，要社會與政府對你的工作尊重。當年的時候你要搞數學的話，如果沒有數學教授的位置，就沒有人付你工資。一個主要的辦法就是得獎金。有幾個科學院它給獎金，得了獎金后你當然可以維持一段時間，因此就很高興。不過很有意思的是我想Riemann-Christofell曲率張量是一個很偉大的發現，黎曼就到法蘭西科學院申請獎金。科學院的人看不懂，就沒有給他。

 

所以諸位，今天坐在前排幾位你們都是得獎人，都是得到光榮的人，我們對于你們寄予很大的期望，后面幾排的大多數人沒有得過獎，不過我安慰大家，沒得過獎不要緊，沒得過獎也可以做工作。我想我在得到學位之前，也沒有得過獎。得不得到獎不是一個很重要的因素，黎曼就沒有得到獎。他的Riemann-Christofell張量在法蘭西的科學院申請獎沒有得到。

 

最近雖然在黎曼幾何上有很多發展，非常了不得的發展，但是大家對于一般的情形，黎曼論文的一般情形、Finsler幾何，沒有做很多貢獻。很巧的是我在1942年曾寫了一篇Finsler幾何的論文，就是找能把黎曼幾何的結果做到Finsler幾何的情形。

 

最近有兩位年輕的中國人，一個叫鮑大維，一個叫沈忠民，我們合寫了一本關于Finsler幾何的書。這本書就要在Springer-Verlag出版，屬于它的GraduateTexts數學叢書。編輯對于我們的書也很喜歡，給了我們一個很有意思的書號：200。書就在這里，我想這本書等會我會交給谷超豪教授，就把它放在復旦大學的某個圖書館里（掌聲）。

 

 

數學學科介紹人谷超豪教授于介紹會講話，圖源：求是科技基金會官網。

 

我們這本書有一個小小的成就，就是把近一百年來最近在黎曼幾何上的發現，我們把它推廣到一般的情形，即黎曼-Finsler情形。這是黎曼當年的目的。黎曼當然非常偉大，不過他對于一般的情形不是很重視，他甚至在他的文章里講這里沒有新的東西，我們就把他說的沒有新的東西做了一些出來。

 

我知道我旁邊坐了兩位偉大的物理學家。接下去我想班門弄斧一下，談一下物理與幾何的關系。我覺得物理學里有很多重要的工作，是物理學家要證明說物理就是幾何。

 

比方說，你從牛頓的第二運動定律開始。牛頓的第二定律說，F＝ma，F是力，m是質量，a是加速度，加速度我們現在叫曲率。所以右邊這一項是幾何量，而力得當然是物理量。所以牛頓費了半天勁，他只是說物理就是幾何（大笑，掌聲）。不但如此，愛因斯坦的廣義相對論也是這樣。愛因斯坦的廣義相對論的方程說：

 

Rik - 1/2 gik R=8πKTik

 

Rik是Ricci曲率，R是scalarcurvature，即標量曲面，K是常數，Tik是energy stress tensor，即能量-應力張量。你仔細想想，他的左邊是幾何量，是從黎曼度量得出來的一些曲率。所以愛因斯坦的重要方程式也就是說，幾何量等于物理量（掌聲）。

 

不止是這些，我們可以一直講下去。我們現在研究的空間叫流形，是一塊塊空間拼起來的。這個流形不好研究。流形上的度量，你如果要把它能夠用方程寫下來的話，你一定要把流形線性化，一定要有一個所謂的向量空間，叫vector space。

 

向量空間有一個好處，它的向量可以相加，可以相減，它還有種種不同的乘法。所以你就可以用解析的方法處理幾何的情形。那么一般的流形怎么處理呢？數學家的辦法很簡單，就是在流形的每一點弄一個切平面。每一點都有個向量空間，叫切空間，跟它相切。

 

歐幾里德空間只有一個切空間。現在的空間情況復雜了一些，每點都有一個切空間，但都是平坦空間。這個現象在幾何上有一個重大的發展，就是把切空間豎起來。反正是一把向量空間，給流形的每點一個向量空間，不一定要是流形的切面或切空間。我們就叫它為纖維叢，或叫向量叢，向量空間叢。這個我想比愛因斯坦的（相對論）還要重要。Maxwell方程就是建立在一個向量叢上。

 

你不是要一把向量空間嗎？最好的是一把筷子，這里一維最好是復一維，complex。這把筷子每個都是復空間，它是騙人的一維，其實是二維，是復數空間。復數就有玩意兒了。現在是一把復數，你如果能有法子從這個纖維到另外一個纖維，有一個我們所謂的平行性的話，你就立刻得到Maxwell方程。

 

現代文明都靠電，控制電的方程的是Maxwell方程。現在纖維叢上有一個平行性，這個平行性的微分，等于電磁場的強度F，然后你把這個F再求它的另外一種微分（余微分）的話，就得到currentvectorJ，即流向量。用下面兩個簡單的式子，就把Maxwell方程寫出來了，dA=F, δF=J。

 

普通你要念電磁學的書的話，當然需要了解電磁的意義。我不了解。但是要了解電磁學的意義，把方程全部寫出來的話，書上往往是一整頁，種種的微分呀什么的講了一大堆。其實簡單地說，也就是平行性的微分是場的強度，而場的強度經過某個運算就得到它的流向量。這就是Maxwell方程，與原來的完全一樣。所以Maxwell方程就是建立在一維的纖維叢上，不過是一個復一維的纖維叢。

 

你怎樣把每個纖維維拼起來呢？我們需要群的概念。有一個群，群里有一個運算，把一個纖維可以挪到其它一個纖維。纖維如果是一維的，即使是復一維的話，我們需要的群仍舊是可交換的群，叫做Abel group，楊振寧先生了不得。他可以用到一個非Abel群，也很簡單，我們叫做SU（2）群。用SU（2）connection，把同樣的方程式寫出來，就是Yang-Mills方程，DA=F，δF=J。

 

這有不得了的重要性。我們搞幾何學的人覺得有這樣的關系，物理學家說你這個關系跟物理有關系，這是非常困難的，并且有基本的重要性。比方說像去年獲諾貝爾獎的，我想大家都知道崔琦的名字，做理論方面的所謂Hall效應，也用到我們這些工作。

 

我們說我們專搞曲率。你要開一個車，路如果彎得多了的話你就要慢下來，直的話你就沖，這就是曲率。曲率要是在高維就比較復雜了，不過也是一些代數，并且可以做得很巧妙。我的一個朋友，也是學生，叫Simons。我們所做的工作就是曲率，就對崔琦跟他們一群得諾貝爾獎的有好處。所以一般講來，在房子里我們只管掃地，想把房子弄弄干凈，弄弄清楚，然后有偉大的物理學家來說你們這個還有道理（大笑，掌聲），這個我們也很高興。

 

現在幾何不僅應用到物理，也應用到生物學中。講到DNA的構造，是一個雙螺線，雙螺線有很多幾何，許多幾何學都在研究這個問題。現在許多主要的大學，念生物的人一定要念幾何。現在有很多人研究大一點的compound，這是分子，是由原子配起來的。原子怎么個配法就是幾何了。這些幾何的觀念不再是空虛的，有實際上的化學的意義。

    

數學比其它科學有利的地方，是它基本上還是個人的工作。即使在僻遠的地方，進步也是可能的。當然他需要幾個朋友，得切磋之益。謝謝大家。（極其熱烈的掌聲）

 

注：本文轉載自求是科技基金會官網。

 

來源：賽先生微信號